1. Biografía
Matemático francés nacido en Beaumont de Lomagne,
una pequeña ciudad francesa el 17 de agosto de 1601. Su padre,
Dominique Fermat, era comerciante de cueros con influencias políticas.
Su madre, Claire de Long, era descendiente de una familia de juristas.
Hay poca información sobre su formación inicial
pero parece probable que hubiera adquirido una sólida instrucción en su
hogar y en el monasterio local de franciscanos en Beaumont.
Posteriormente estudió leyes en la universidad de Tolouse y entre 1625
y 1630 se trasladó a Bordeaux donde comenzaron sus investigaciones
matemáticas serias. De Bordeaux se trasladó a Orléans donde se graduó
en leyes en 1631.
A los 30 años fue nombrado magistrado en Toulose,
donde ocupó el cargo de consejero del parlamento local desde 1648. Se
casó con una prima de su madre, Louise de Long, con la que tuvo tres
hijos y dos hijas. Uno de los hijos fue el responsable de recopilar sus
trabajos matemáticos para publicarlos pues Fermat no publicó ningún
trabajo matemático durante su vida.
Murió el 12 de enero de 1648 en Castres, cerca de
Toulouse.
2. Fermat y las
matemáticas
Fermat, abogado sólo se dedicó al estudio de las
matemáticas por afición. Tampoco publicó ninguno de sus resultados ni
de sus métodos, los cuales se encontraron en hojas sueltas después de
su muerte. Aún así, su contribución a la formación de la geometría
analítica, el cálculo de probabilidades y a la aritmética moderna a
sido decisiva para el desarrollo de las matemáticas. Además anticipó el
cálculo diferencial con su método de búsqueda de máximos y mínimos de
las líneas curvas con rectas tangentes.
Desde joven las obras de Apolonio suscitaron su
interés por la teoría de lugares geométricos y concibió (antes que
Descartes) la noción fundamental de la geometría analítica al
representar las curvas por ecuaciones.
Pero si Fermat destaca por algo es por su afición
a la teoría de números y por su conocido “último teorema de Fermat”.
Entre otros problemas estudió los números primos, los números amigos y
los números perfectos.
2.1. Números primos
Números primos son aquellos que sólo son
divisibles por uno y por sí mismos. Por ejemplo, los primeros números
primos son 2, 3, 5, 7, 11, 13, 17, 19, ...
Un problema interesante desde el punto de vista de
las matemáticas es averiguar si un número cualquiera es primo o no.
Para ello, en el Instituto se utiliza el llamado “método de las
divisiones” que consiste en ir dividiendo el número por los primos más
pequeños. El inconveniente es que supone realizar muchas operaciones.
Una forma de saber si un número es o no primo
sería tener una fórmula. Ésto hasta ahora no ha sido posible, sin
embargo Fermat ya estudió este problema y concluyó que los números que
resultan de la fórmula 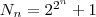 son primos y así obtuvo los
llamados números
primos de Fermat o de Mersenne. Los primeros son: son primos y así obtuvo los
llamados números
primos de Fermat o de Mersenne. Los primeros son:

Fermat tras observar que los primeros números de
esta fórmula eran primos creyó que todos lo serían. Sin embargo, en
1739, Euler encontró un número de Fermat que tenía un divisor y, por lo
tanto, que no era primo.
2.2. Números perfectos
Un número es perfecto si es igual a la suma de sus
divisores exceptuando él mismo. Por, ejemplo el número 6 es perfecto,
pues sus divisores, 1, 2, 3 y 6 sumados (sin sumar el 6) 1+2+3=6.
Otro ejemplo de número perfecto es el 28, cuyos
divisores son 1, 2, 4, 7, 14, y 28. Al sumarlos (sin el 28) se obtiene
1+2+4+7+14=28. Otros ejemplos de números perfectos son el 496 y el 8128.
El problema consiste ahora en hallar una regla que
permita encontrar números perfectos, y que sea útil también para
deducir si un número es o no perfecto. Este problema fue propuesto por
Mersenne en una carta a Descartes. Fermat descubrió un número en el que
la suma de sus divisores es múltiplo del número (estos números se
llaman perfectos por múltiplos). Este número es el 672. Más tarde
Descartes descubrió el 1.476.304.896.
2.3. Números amigos
Fermat obtuvo una complicada fórmula para obtener
números amigos. Esta fórmula afirma que para cualquier número n
mayor que
1, si los números 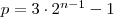 , , 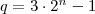 y y 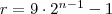 son los tres primos, entonces
los números son los tres primos, entonces
los números 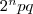 y y 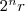 son
amigos. Con esta fórmula Fermat fue capaz de deducir que 17296 y 18416
son amigos. son
amigos. Con esta fórmula Fermat fue capaz de deducir que 17296 y 18416
son amigos.
3. El último teorema
de Fermat
 El
resultado más famoso de Fermat se halló en un libro. Exactamente en el
margen de un libro que Fermat solía estudiar llamado Aritmética
de
Diofanto. Este teorema está relacionado con las ternas pitagóricas
(tres números que cumplen la ecuación El
resultado más famoso de Fermat se halló en un libro. Exactamente en el
margen de un libro que Fermat solía estudiar llamado Aritmética
de
Diofanto. Este teorema está relacionado con las ternas pitagóricas
(tres números que cumplen la ecuación 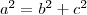 ) como por ejemplo 3, 4 y 5.
Fermat propuso que si el exponente deja de ser 2, no hay ninguna terna
de números que cumplan la relación ) como por ejemplo 3, 4 y 5.
Fermat propuso que si el exponente deja de ser 2, no hay ninguna terna
de números que cumplan la relación 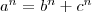 . Al descubrir esto, Fermat
escribió
en los márgenes de su libro: “He descubierto una demostración
extraordinaria de esto que no cabe porque este margen es demasiado
pequeño”. . Al descubrir esto, Fermat
escribió
en los márgenes de su libro: “He descubierto una demostración
extraordinaria de esto que no cabe porque este margen es demasiado
pequeño”.
Lo cierto es que muchos matemáticos han querido
demostrar que el teorema de Fermat era cierto o encontrar una excepción
para probar que era falso. Tan difícil resultaba que en 1908 (más de
250 años después) se estableció un premio de 100000 marcos para quien
fuese capaz de encontrar una demostración antes del 13 de septiembre de
2007. Finalmente el teorema de Fermat fue demostrado, en la década de
los 90 del pasado siglo, y depués de muchos intentos, por el matemático
inglés Andrew Wiles.
Bibliografía
- http://centros5.pntic.mec.es/ies.salvador.dali1/primeroa/fermat
- http://www.mat.usach.cl/histmat/html/ferm.html
- Microsoft Encarta Biblioteca de Consulta
2003.
- Torrecillas Jover, Blas “Fermat. El mago de los
números”.Nivola 2003.
|

