| Los matemáticos de la relatividad por Alumnado de 4º de ESO A IES Antonio de Mendoza |
|||||||||||||||||||||||||||||||||||||||||||||
| Se presentan pequeñas biografías de matemáticos ilustres de los siglos XIX y XX que, bien por su influencia sobre Einstein, por ser coetáneos o por haber participado de forma activa en la investigación, son referentes en el desarrollo de la Teoría de la Relatividad. Los trabajos se han realizado de forma independiente por alumnos de 4º ESO A. Gauss, Gödel, Hilbert, Levi-Civita, Poincaré, Ricci-Curbastro, Riemann y Von Neumann |
|||||||||||||||||||||||||||||||||||||||||||||
| Carl Friedrich Gauss (1777-1855) Francisco José Heredia 
Georg Friedrich Bernhard Riemann (1826-1866) Las ideas de Riemann concernientes a la geometría del espacio tuvieron profundos efectos en el desarrollo de la teoría física moderna. Clarificó la noción de Integral, definiendo lo que ahora llamamos Integral de Riemann. Riemann se trasladó de Gottingen a Berlín en el año 1846 para estudiar bajo la enseñanza de Jacobi, Dirichlet y Eisenstein. El año 1849 retornó a Gottingen y su tesis supervisada por Gauss fue presentada en el año 1851. En su informe de la tesis, Gauss describe a Riemann como alguien que tenía una fácil y gloriosa originalidad. Con las recomendaciones de Gauss, Riemann fue nominado para un puesto en Gottingen. Los escritos de Riemann de 1854 llegaron a ser un clásico en las matemáticas y sus trabajos fueron incorporados dentro de la teoría de la relatividad y gravitación de Einstein. La cátedra de Gauss en Gottingen fue ocupada por Dirichlet en el año 1855 y, después de la muerte de éste por Riemann. En esos tiempos sufrió de tuberculosis y estuvo sus últimos años en Italia en un intento por mejorar su salud. Las ideas de Riemann concernientes a la geometría del espacio tuvieron un profundo efecto en el desarrollo de la teoría física moderna y proveía los conceptos y métodos usados después en la Teoría de la Relatividad. Fue un pensador original y un descubridor de los métodos, teoremas y conceptos que llevan su nombre. Las ecuaciones de Cauchy-Riemann y el concepto de la superficie de Riemann aparecieron ya en su tesis de Doctorado. Este matemático demostró que una geometría en la que no existen líneas paralelas también es posible. Los detalles de estos dos tipos de geometría no euclídea son complejos, pero ambos se pueden demostrar utilizando modelos sencillos. Geometría no euclídeaLa geometría de Bolyai-Lobachevski, llamada normalmente geometría no euclídea hiperbólica, describe la geometría de un plano que está formado sólo por los puntos interiores de un círculo en el que todas las posibles líneas rectas son cuerdas del círculo. En ésta, se puede dibujar un número infinito de líneas paralelas a una línea L que pasen por un punto P sin que se corten. De la misma manera, la geometría riemanniana o no euclídea elíptica, es la geometría de la superficie de una esfera en la que todas las líneas rectas son círculos máximos. En esta geometría es imposible dibujar un par de líneas paralelas en el sentido clásico. Gregorio Ricci-Curbastro (1853-1925) Su publicación más famosa, El cálculo diferencial absoluto, fue publicada bajo el nombre de Ricci y como co-autor su ex-estudiante Tullio Levi-Civita. Esta parece ser la única vez que Ricci-Curbastro utilizó la forma acortada de su nombre en una publicación, y continúa causando confusión. Tensor de Ricci dirigido por la curvatura de RicciLa curvatura de Ricci se puede utilizar para definir las clases de Chern de una variedad, que son invariantes topológicos (por tanto independientes de la elección de métrica). La curvatura de Ricci también se utiliza en el flujo de Ricci, donde una métrica es deformada en la dirección de la curvatura de Ricci. En superficies, el flujo produce una métrica de curvatura de Gauss constante y se sigue el teorema de uniformización para las superficies. La curvatura de Ricci desempeña un papel importante en relatividad general, donde es el término dominante en la ecuación de campo de Einstein. Henri Poincaré (1854-1912) Nació el 29 de abril de 1854 en Nancy, al nordeste de Francia. Sorprendentemente se sabe poco de su madre. Su padre Léon, médico, ejerció su profesión durante toda su vida en Nancy, de cuya facultad de Medicina también fue profesor. Henri pertenecía a una familia bastante ilustre, su tío Antoine fue inspector General de Caminos y Puertos y los dos hijos de éste, Raymond que llegó a ser presidente de la República durante la Primera Guerra Mundial y Lucien, director general de Enseñanza Secundaria. Poincaré y las matemáticasLas contribuciones de Poincaré a la matemática fueron tan numerosas que es difícil resumirlas. Prácticamente estudió todos los temas de la matemática de la época: ecuaciones diferenciales, teoría de números, análisis complejo, mecánica, astronomía, física matemática. No obstante, hay algunos temas que no podemos olvidar, como sus trabajos sobre las funciones automorfas. Casos particulares de funciones automorfas habían sido estudiados antes de Poincaré (por ejemplo, funciones periódicas) pero las generalizaciones que este introdujo revelaron la existencia de funciones hasta ahora desconocidas, como las zeta-fuchsianas, que además podían ser utilizadas, como demostró él mismo, para resolver ecuaciones diferenciales lineales de segundo orden con coeficientes algebraicos (Poincaré comenzó a trabajar en este tema a raíz de la convocatoria, en 1880, de un premio por parte de la Académie des Sciences, que tenía como tema el de “Perfeccionar en cualquier punto importante la teoría de ecuaciones diferenciales ordinarias de una sola variable independiente”). Uno de los matemáticos que habían trabajado en el campo de las funciones automorfas antes que Poincaré era Félix Klein (1849-1925). Profesionalmente Poincaré ocupó las cátedras de Física matemática y Astronomía matemática de la Sorbona. Nuestro matemático tenía por costumbre tratar un tema distinto en cada uno de sus cursos y afortunadamente el contenido de dichos cursos se publicaba redactado por alguno de sus colaboradores, aunque corregía personalmente las pruebas. Es así como contamos con obras como: Potentiel et mécanique des fluides (curso académico 1885-1886), Théorie mathématique de la lumière I (1887-1888), Thermodynamique(1888-1889), Electricité et optique: I. Les théories de Maxwell et la théorie électromagnétique de la lumière y II. Les théories de Helmholtz et les expériences de Hertz (1888-1889). Método y CienciaPoincaré no fue sólo un gran científico, sino también un perspicaz y profundo pensador; prueba de ello la tenemos en libros como: La ciencia y la hipótesis (1902), El valor de la ciencia (1905), Ciencia y método (1908) y Últimos pensamientos (1913), una recopilación de artículos que había publicado anteriormente. En estos libros, el autor, nos familiariza con la crisis de fundamentos que afectó a la matemática a finales del siglo XIX y cuyas consecuencias ni siquiera él pudo adivinar. Captamos la gravedad de los problemas que plantean los descubrimientos físicos del último tercio del siglo pasado y que llevarían a la formulación de la teoría de la relatividad especial y a una nueva manera de entender la naturaleza del espacio y del tiempo, hallazgos de los que no estuvo muy alejado Poincaré. En Ciencia y método se plasman las ideas que sobre la naturaleza de la matemática y el razonamiento matemático tenía Poincaré. Su genio e intuición eran tales que es posible encontrar grandes tesoros conceptuales en rincones aparentemente menores. Así tenemos que adivinó la posibilidad de la existencia del caos, una de las ramas de la matemática y física contemporánea, así como sus características principales. Algunas frases célebres de Henri Poincare Probamos por medio de la lógica, pero descubrimos por medio de la intuición.
Una palabra bien elegida puede economizar no solo cien palabras sino cien pensamientos.
David Hilbert (1862-1943) Nacido en Königsberg, al este de Prusia (hoy Kaliningrado, Rusia), Hilbert estudió y permaneció en Konisgsberg hasta los 33 años, enseñando e investigando en la universidad local. En 1895 fue llamado por Félix Klein para ocupar un puesto de profesor en la Universidad de Gotinga, donde estuvo hasta el resto de sus días y donde convirtió a la ciudad en el centro de las matemáticas alemanas, y probablemente de las mundiales. Trabajó en muchos campos de las matemáticas, incluyendo la teoría de números y el cálculo de variaciones, pero sus más importantes contribuciones las hizo en el terreno de la geometría. En 1899 con su obra Fundamentos de la geometría, reemplazó eficazmente la geometría euclídea con un conjunto de 21 axiomas mucho más completos y abstractos, que tratan sobre puntos, líneas y planos y seis tipos de relaciones entre ellos. En la Conferencia Internacional de Matemáticos que tuvo lugar en París en 1900, el matemático alemán expuso sus teorías. Hilbert había contribuido de forma sustancial en casi todas las ramas de las matemáticas. La conferencia de Hilbert en París consistió en un repaso a 23 problemas matemáticos. Los Problemas que propuso representaban a su entender los puntos esenciales de investigación que harían progresar las matemáticas a lo largo del siglo; la mayoría ya han sido resueltos, gracias a las discusiones suscitadas sobre ellos han servido para permitir la evolución de las matemáticas modernas. Hilbert comenzó estudiando los variantes algebraicos sobre los que escribió su tesis doctoral, culminando su trabajo con una demostración del teorema de la base de Jordan. Continuó el cálculo de variaciones, las ecuaciones integrales, el análisis funcional y la física matemática, aportando resultados de gran importancia en todos ellos. La última etapa investigadora de Hilbert, ya a una edad avanzada, fue su famosa intervención en la disputa sobre los fundamentos: la formulación del programa de Hilbert, que daba un giro realmente novedoso al tema. Las actitudes de Hilbert sobre los fundamentos evolucionaron desde una preferencia inicial por el logicismo de Dedekind en los años 1890. Tras la primera Guerra Mundial, las críticas a la matemática “clásica” planteadas por Brouwer y Weyl le motivaron a intentar “eliminar de una vez por todas las dudas escépticas sobre las matemáticas”. Sin olvidar nunca el contenido conceptual de las teorías matemáticas ni la importancia de la intuición, Hilbert apostó por resolver el problema de los fundamentos combinando la axiomática con la nueva lógica formal. Esto permitía una formalización completa de las teorías matemáticas conocidas, y el desarrollo de una teoría de la demostración que consideraba las demostraciones como resultado de meras combinaciones de símbolos según reglas formales prescritas. Ahora, bastaba demostrar que ninguna derivación formal, ninguna combinación de símbolos podía conducir a la fórmula El trabajo sobre este tema en los años 1920 fue esencial para la maduración definitiva de la lógica matemática y para el surgimiento de las teorías de la computación. Fue una obra colectiva, con el gran lógico Paul Bernays como colaborador imprescindible de Hilbert y con figuras de la talla de von Neumann realizando aportaciones originales. Es bien sabido cómo la genial contribución de Kurt Gödel en 1931 puso fin al proyecto de demostrar la consistencia de la aritmética de Peano por medios finitos. De todos modos, la aportación del maestro y su entusiasmo lograron mantener el rumbo del gran barco de las matemáticas: pese a que las dudas escépticas nunca fueron erradicadas del todo, la matemática “clásica” siguió gozando de la mejor salud. Además, no hay que olvidar el poderoso desarrollo de la lógica matemática posterior, ni sus decisivas aplicaciones tecnológicas en el mundo de los ordenadores. Tullio Levi-Civita (1873-1941) Introducción Su libro de texto de cálculo tensorial El Cálculo Diferencial Absoluto (originalmente un conjunto de notas de la conferencia en italiano de coautoría con Ricci-Curbastro) sigue siendo uno de los textos de referencia más de un siglo después de su primera publicación, con varias traducciones disponibles. Carrera profesionalLevi-Civita se graduó en la universidad de Padua, donde coincidió con Ricci el cual fue uno de sus profesores. Levi-Civita accedió a la Cátedra de Mecánica en Padua en 1898, puesto que ocupó durante 20 años. En 1918 accedió a la cátedra de la misma especialidad en Roma, donde pasó otros 20 años hasta que fue cesado por la política de discriminación del gobierno (él era judío). En 1887 publicó un artículo famoso en el cual desarrolló el cálculo de tensores, siguiendo el trabajo de Christoffel, e incluyendo la diferenciación del tensor covariante. Otro tema que interesó a Levi-Civita fue la dinámica analítica. Muchos de sus artículos examinaban casos especiales del problema de tres cuerpos. También escribió sobre la hidrodinámica y la teoría de los sistemas de ecuaciones diferenciales parciales, que aplicó a la teoría de Cauchy y de Kovalevskaya y preparó este trabajo en un libro excelente escrito en 1931. La Royal Society le concedió la medalla de Sylvester en 1922, mientras que en 1930 lo eligieron como miembro extranjero. También fue miembro honorario de la Sociedad Matemática de Londres, de la Sociedad Real de Edimburgo, y de la Sociedad Matemática de Edimburgo. Durante su vida, Levi-Civita, al igual que Volterra y muchos otros científicos italianos, se opuso fuerte y activamente al fascismo. Después de que, por razones políticas, le retirasen todos sus títulos y su cátedra, se hundió emocionalmente y desarrolló problemas severos de corazón. Murió de un derrame cerebral alejado del mundo científico. Relaciones con Albert EinsteinCuando en 1914 Einstein publicó su primer artículo de la relatividad general, dicho artículo cayó en manos de Max Abraham, un competidor de la época en el tema, que no entendió la teoría por su complejidad matemática. Así, se la enseñó a Levi-Civita para que le explicara cómo podía interpretarla. Levi-Civita, como hemos visto todo un especialista en tensores, al tener noticia de la Relatividad General se interesó por ella, la estudió y encontrando un fallo en ésta, en 1915 escribió una carta a Einstein comunicándoselo. El fallo consistía en un cambio de base que Einstein había demostrado de forma no muy rigurosa. Una posible razón es que Einstein no era matemático, sino físico, y la intuición y la lógica le decían que lo que había hecho era correcto, sin embargo la demostración era incorrecta, y ese es el punto donde Levi-Civita le corrigió. Einstein le respondió con otra carta diciendo que en un principio se había asustado mucho, porque uno de los pilares de la teoría estaba en ese cambio de base, pero que revisándolo con detalle podría resolver los problemas con que se había encontrado. Doce días más tarde le escribió una segunda carta en la que el error estaba corregido y en la que le pedía, entre otras cosas, que le contestara en italiano, ya que Einstein había estado en Italia y le había gustado el idioma. A partir de ese momento, se inició un largo e interesante intercambio de cartas entre Einstein y Levi-Civita. Einstein tiraba toda su correspondencia, sin embargo, Levi-Civita, mucho más metódico, guardaba todas las cartas que recibía; de ahí que se haya podido conservar el texto de todas ellas para la historia. Entre estas cartas y las que sucedieron después pueden leerse textos escritos por Einstein del tipo: Jamás había tenido una correspondencia tan interesante como ésta o No sabe lo ansiosamente que espero sus cartas. El trabajo de Levi-Civita fue extremadamente importante en el desarrollo posterior de la teoría de la Relatividad General. Pero Italia y Alemania entraron en guerra, y la correspondencia entre los dos científicos se detuvo durante 2 años. En 1917 Levi-Civita recibió, después de esos 2 años, una postal de Einstein en la que afirmaba que se había llevado toda la documentación consigo a EEUU para estudiarla con detalle. También le decía en esta postal que admiraba la elegancia de su método de cálculo. La controversia había perdido importancia y lo que buscaban estos dos hombres era una razón para seguir manteniendo el contacto. Por fin, en 1921, pasada la guerra, Einstein y Levi-Civita se conocieron en Bolonia. Años más tarde, en 1936, Einstein invitó a Levi-Civita a Princeton, donde vivió todo un año. Pero, en 1938, las nubes de la guerra volvieron a aparecer. John Von Neumann (1903-1957) Von Neumann fue un gran matemático. Destacó por sus aportaciones fundamentales a la teoría cuántica, especialmente el concepto de anillos de operadores (actualmente conocido como álgebra de Neumann) y por su trabajo en la teoría de juegos. John von Neumann es considerado como el padre de la teoría de juegos. En una serie de artículos entre 1920 y 1930, estableció la estructura matemática de todos los desarrollos teóricos posteriores. En la teoría de juegos, la palabra juego se refiere a un tipo especial de conflicto en el que toman parte n individuos o grupos (conocidos como los jugadores). Hay ciertas reglas del juego y se distinguen dos tipos de juegos:
Planteó la posibilidad teórica de que un programa informático se reprodujera. Poco despues aparecieron los virus informáticos. Participó también en el desarrollo de los ordenadores a través del trabajo en hardware como en software. Algunas obras de John von Neumann de especial interés en la economía son Zur Theorie der Gessellshaftspiele (1928), A Model of General Economic Equilibrium (1937), Theory of Games and Economic Behavior (1944), A Communications on the Borel Notes (1953), Solutions of Games by Differential Equations (1953), Two Variants of Poker (1953), A Numerical Method to Determine Optimum Strategy (1954) o The Computer and the Brain (1958). Kurt Gödel (1906-1978) Sobresalió en el trabajo escolar. Su primer interés académico fue Lingüística, pero más tarde acudió a las Matemáticas ya que era más fácil para él estudiarlas por su cuenta, una vez agotados los recursos que le ofrecía la escuela. Ingresó en la Universidad de Viena en 1924 planeando estudiar Física Teórica. Hacia 1926 su atención volvió a las Matemáticas y se produjo su unión a lo que más tarde fue conocido como el Círculo de Viena, un grupo de matemáticos que fundó la escuela filosófica conocida como Positivismo Lógico. Gödel estuvo asociado con este grupo durante muchos años. La principal premisa del Círculo de Viena era que lo que no es verificable empíricamente no tiene sentido. La antítesis de esta filosofía es la especulación metafísica, ya que nada puede ser probado o refutado con algún grado de certidumbre dentro del sistema metafísico. Gödel se fue interesando progresivamente en la Teoría de Números y, después, en Lógica Matemática durante estos años. A partir de 1928 raras veces participó en las reuniones del Círculo de Viena. En 1930, Gödel se doctoró en Matemáticas dirigido por H. Ham, un notable matemático miembro del Círculo de Viena. A partir de aquí comienza Gödel a trabajar en sus más importantes teorías sobre la completitud de sistemas formales. Viajó a los Estados Unidos dando un ciclo de conferencias y se encontró por primera vez con Albert Einstein en 1933. Dedicó alguno de los años siguientes al estudio de problemas de Física y de Psicología. Durante esta época tuvo que ser ingresado varias veces en hospitales por problemas de salud. En 1931 Kurt Gödel fue capaz de responder a dos de las preguntas formuladas por David Hilbert en el Congreso Internacional de Matemáticos de 1900, demostrando que cualquier sistema formal suficientemente potente es inconsciente o incompleto. Así mismo probó que si un sistema de axiomas es consistente, esta consistencia no puede demostrarse por sí misma. Gödel se casó con Adele Porket en 1938 y decidieron trasladarse definitivamente a los Estados Unidos en 1940. Se asentaron en Princeton, New Jersey, donde residieron hasta el final de sus vidas. Durante estos años daba un paseo diario con otro ilustre refugiado y colega, Albert Einstein. Relaciones con EinsteinLlegó a ser un gran amigo de Einstein, y trabajaron juntos los aspectos filosóficos y matemáticos de la Teoría General de la Relatividad. Gödel incluso trabajó con éxito en las ecuaciones del campo gravitatorio, encontrando soluciones sorprendentes. También dedicó gran parte de su tiempo al estudio del concepto de tiempo, publicando varios artículos y dando varias conferencias sobre el tema. Recibió muchos homenajes importantes durante su vida. Fue nombrado doctor honoris causa en Literatura por la Universidad de Yale en 1951. También fue doctor honorario en Ciencias por Harvard en 1952 con una mención que lo llamó “el descubridor de la verdad matemática más significativa del siglo”. Fue elegido como miembro de la Academia Nacional de Ciencias en 1955 y de la Academia Americana de las Artes y Ciencias en 1957. En 1961 ingresó en la Sociedad Filosófica de América. En 1967, fue elegido miembro honorario de la Sociedad Matemática de Londres. Finalmente, en 1975, el presidente Ford le entregó la Medalla Nacional de las Ciencias. Batalló durante toda su vida contra sus problemas de salud física y mental. Confesó en 1969 que no entendía el trabajo de los nuevos lógicos; la enfermedad iba cobrando su peaje. En su vejez cuidó con abnegación ejemplar a su esposa, a quien un ataque cardiaco dejó invalida. Temeroso de ser envenenado dejó de comer y murió por desnutrición el 14 de enero de 1978. Su obra es escasa pero la influencia y repercusión de sus trabajos ha sido y será formidable por que afectan a todas las ramas de la lógica moderna. |
|||||||||||||||||||||||||||||||||||||||||||||
Nació el 17 de septiembre de 1826 en Hannover (Alemania) y falleció el 20 de julio de 1866 en Selasca (Italia).
Jules Henri Poincaré (1854-1912) fue uno de los matemáticos más importantes del siglo XIX y comienzos del XX. Nos encontramos ante un científico que captó con profunda claridad y gran sencillez la esencia del método científico, teniendo además las dotes necesarias para exponer y transmitir al gran público sus ideas metodológicas y epistemológicas. Se planteó problemas como la naturaleza de la matemática y del razonamiento matemático y qué consecuencias se derivan de la “Nueva Mecánica” que parecía imponer el desarrollo de la teoría electromagnética.
Sin duda se trata del matemático más famoso del siglo XX, a lo que contribuyeron de manera muy especial su aportación a la configuración de los métodos axiomáticos actuales, sus profundos resultados en álgebra, teoría de números, geometría y teoría de funciones, los celebérrimos “problemas matemáticos” que dejó planteados en 1900, y las venturas y desventuras de sus intentos de resolver la cuestión de los fundamentos de la matemática. En el año de su muerte, se le celebraba como aquel “a quien el mundo consideró durante las últimas décadas como el más grande matemático vivo”.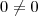
y con ello quedaría establecida la consistencia de la teoría formal estudiada.
Tullio Levi-Civita nació el 29 de marzo de 1873 en Padua, Italia, y murió el 29 de diciembre de 1941 en Roma, Italia. Fue un matemático italiano, famoso por su trabajo sobre cálculo tensorial que también hizo contribuciones significativas en otras áreas. Era un discípulo de Gregorio Ricci-Curbastro, el inventor (algunos dicen co-inventor junto con él) del cálculo tensorial. Su trabajo incluye artículos fundamentales en matemáticas puras y aplicadas, la mecánica celeste (notablemente en problema de tres cuerpos) e hidrodinámica.
John von Neumann, matemático estadounidense nacido en Hungría, desarrolló la rama de las matemáticas conocida como teoría de juegos. Natural de Budapest, estudió en Zurich y en las universidades de Berlín y Budapest. En marzo de 1955 fue nombrado miembro de la Comisión de Energía Atómica de los Estados Unidos.
Kurt Gödel nació el 28 de abril de 1906 en Brünn, Moravia. Su padre, Rudolph, fue un diligente e inventivo propietario de una fábrica textil. Su madre, Marianne, fue una cariñosa madre de familia que había recibido una extensa educación literaria en Francia. La familia de Gödel era económicamente acomodada y el joven Kurt pudo dedicar todas sus energías al estudio, ya que no era necesario colaborar en la financiación familiar.