| Regresión no paramétrica. Estimación no paramétrica de la función de distribución discontinua por Ismael Ramón Sánchez Borrego Departamento de Estadística e Investigación Operativa. Universidad de Granada |
 |
| Introducción En el estudio de las variables bidimensionales y en general, de las multidimensionales, puede resultar interesante investigar la posible existencia de una relación de dependencia entre las variables unidimensionales y la construcción de algún modelo matemático que permita describir dicha relación, en el supuesto de que ésta exista.
Así por ejemplo, es bien conocido que el radio X y la longitud Y de una circunferencia están relacionados mediante el modelo Sin embargo, existen situaciones en las que la variable X contiene cierta información (incompleta) acerca de la variable Y, pudiéndose predecir aproximadamente el valor de Y a partir del conocimiento del valor que ha tomado X mediante la construcción de lo que llamamos modelos de regresión. Por ejemplo, la estatura X de una persona no determina completamente su peso Y, pero es claro que si conocemos la estatura somos capaces de predecir aproximadamente el peso. El propósito del estudio de los modelos de regresión es la construcción de modelos matemáticos que permitan explicar la relación de dependencia existente entre una variable respuesta, Y y una o más variables independientes X. A partir de esto, podemos utilizar estos modelos como herramienta para predecir nuevos valores de la variable respuesta a partir de cierto valor particular que ha tomado la variable explicativa. Es imprescindible el empleo de estos modelos cuando se pretende predecir una variable respuesta que es imposible o muy costosa de medir. Por ejemplo, podemos considerar un modelo de regresión lineal para predecir el peso Y a partir de la altura X según la función lineal:
Podemos observar en dicha figura el ajuste satisfactorio que la función de regresión lineal realiza sobre este conjunto de datos. Regresión no paramétricaDadas n observaciones de dos variables bidimensionales (X,Y), consideramos el modelo de regresión
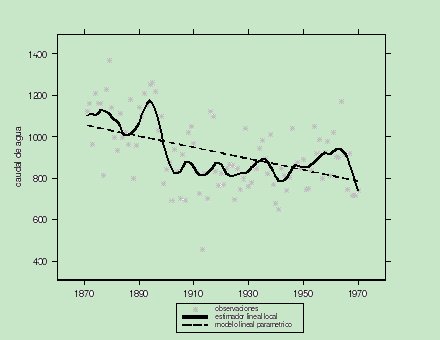
donde E es el error cometido en la predicción de Y a partir de X a través de la función de regresión m. Podemos distinguir dos tipos de modelos de regresión atendiendo a los supuestos que establecen sobre la función de regresión m. En un modelo de regresión paramétrica se asume que la función de regresión tiene una forma predeterminada (lineal: En regresión no paramétrica destaca el estimador de la función de regresión llamado estimador lineal local, introducido entre otros por Fan y Gijbels (1996), que destaca por sus buenas propiedades frente a otros estimadores clásicos. En la Figura 2 podemos apreciar el gráfico que representa las observaciones del caudal de agua del río Nilo en Asuán (Egipto) desde los años 1871 a 1970. Antes de la construcción de la presa de Asuán, el caudal de agua y las crecidas del río Nilo tenían una importancia capital sobre la economía de Egipto. En la Figura 2 podemos observar que la representación de las observaciones (diagrama de dispersión) no parecen presentar la forma de alguna función matemática conocida y sencilla. Si empleamos el modelo habitual lineal de regresión paramétrica (representado por la línea a trozos) y el estimador lineal local (línea continua) podemos observar que éste último proporciona un mejor ajuste a los datos y por tanto una mayor capacidad predictiva (la cantidad E será menor en cada observación , o está más cerca de Y).
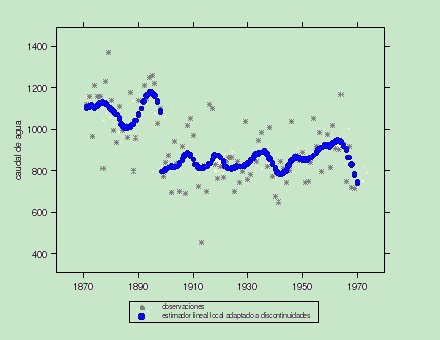
Los métodos no paramétricos son más apropiados cuando no se tiene conocimiento previo de la relación entre las variables objeto de estudio puesto que sólo parten de supuestos de suavidad sobre la función de regresión. Estos métodos no paramétricos son computacionalmente costosos debido al gran número de operaciones que involucran y son sólo aplicables en la práctica con la ayuda de un programa informático. Presento a continuación el problema que afronté en mi tesis doctoral: el problema de estimación de la función de regresión discontinua. El problema de estimación de la función de regresión discontinua Existen numerosas situaciones y problemas reales en los que la función de regresión presenta discontinuidades, como puede ser por ejemplo el caso del efecto de un medicamento en una persona o del impacto de un anuncio publicitario. Uno de los ejemplos clásicos más utilizados por investigadores en este campo es el conjunto de datos del caudal del río Nilo. Este conjunto de datos ha sido estudiado entre otros por Cobb (1978), que localiza una discontinuidad de salto en el año 1898. Debido a los supuestos de suavidad sobre la función de regresión de los que parte el estimador lineal local, este estimador proporciona estimaciones suaves (y por tanto continuas), por lo que la estimación resultante no contempla las discontinuidades de la función de regresión. Este hecho puede observarse en la Figura 2, en la que a pesar de la existencia de un punto de salto en el año 1898, el estimador lineal local tipo núcleo presenta una estimación continua que no recoge dicha discontinuidad. Esta fue una de las aportaciones que realicé en mi tesis doctoral: proponer una modificación del estimador lineal local adaptado a las discontinuidades de salto. Este nuevo estimador es continuo en las regiones de continuidad del estimador lineal local, pero a diferencia de éste, contempla los puntos de salto de la función de regresión, como puede observarse en la Figura 3.
El entorno informático en el que desarrollé los programas informáticos que generan y simulan estos estimadores es R, de libre distribución en la página http://www.r-project.org. Se puede completar y ampliar la información sobre este trabajo en: http://www.springerlink.com/content/24x567272p052km6/; también en esta otra dirección: en http://compstat2004.cuni.cz/c04-awards.htm, (Premio Mathemathica Award en el Symposium COMPSTAT 2004), o simplemente contactando con el autor en la dirección de correo electrónico (ismasb@ugr.es). |
|
|
Bibliografía |
|
|
Sobre el autor Actualmente formo parte del grupo de investigación «Estadística computacional y aplicada”, FQM-145. Las líneas de investigación en las que trabajo en la actualidad son regresión no paramétrica y muestreo. Son varios las trabajos que tengo publicados en estos dos campos. En la actualidad, además de las dos líneas antes mencionadas participo en un proyecto de investigación denominado «Delito contra el medio ambiente e infracciones administrativas medioambientales. Análisis de las actuaciones de ingeniería y de la actividad empresarial”, en el que estudiamos infracciones cometidas sobre el medio ambiente por empresas para el futuro desarrollo de normativa sobre contravenciones medioambientales. Este proyecto nos ha sido concedido recientemente por el Ministerio de Educación y Ciencia y en él soy el responsable de las encuestas por muestreo del mismo. Además, he participado a lo largo de estos años en varios Proyectos de Innovación Docente, donde hemos publicado varios libros sobre Estadística para la Biología, en los que se ha elaborado material teórico-práctico de aprendizaje de la Estadística para el alumno en la licenciatura en Biología, así como supuestos prácticos resueltos con el programa estadístico SPSS. Recientemente hemos desarrollado un programa emulador de SPSS esto es, una aplicación que simula al programa SPSS y que tiene por objetivo facilitar el aprendizaje de la Estadística con SPSS en Biología. El programa está implementado en Java y cuenta con un sistema de ayuda interactiva que guía al alumno cuando comete un error y que le asesora estadísticamente en la interpretación de los resultados. Se puede descargar gratuitamente junto con material didáctico, desde la dirección web: http://www.ugr.es/~bioestad. |
|
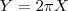(para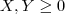 
), de manera que conocido el valor del radio de una circunferencia, somos capaces de predecir con exactitud el valor de su longitud. En esta situación una variable contiene toda la información sobre la otra.
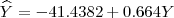(ver Figura 1), que permite obtener un valor estimado del peso de una persona de la que conocemos su altura. Cada asterisco en la Figura 1 representa una pareja de observaciones 
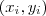de las variables altura (X) y peso (Y).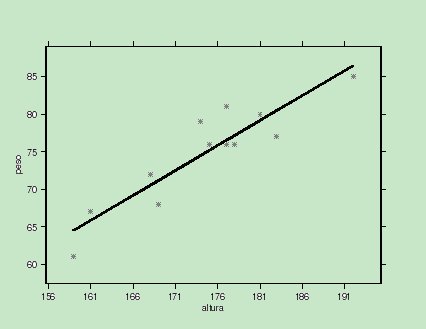
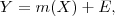
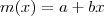, parabólica: 
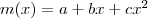, etc). Un modelo de regresión no paramétrica sólo supone hipótesis de suavidad (en el sentido de continuidad y diferenciabilidad) sobre la función de regresión . En el contexto de la regresión no paramétrica no se asume ninguna forma predefinida como las anteriores para la función de regresión.
