| Sobre las dimensiones del Universo por María del Carmen Murcia Cano Alumna de 4º de ESO del IES Antonio de Mendoza |
|
| Si no puedo dibujarlo, es que no lo entiendo (Albert Einstein) | |
 Sería muy difícil diseñar un ser viviente que pudiese existir en solo dos dimensiones. La comida que la criatura no pudiera digerir, debería escupirla por el mismo sitio por el que entró. Si hubiese un pasaje que atravesase al animal a lo largo, tal y como nosotros tenemos, el pobre animal acabaría deshecho en dos partes.
De modo que tres dimensiones, parecen ser las mínimas exigibles para la vida. Pero así como se puede pensar en seres de dos dimensiones viviendo sobre la superficie de la Tierra, también cabria imaginar que el espacio tridimensional en el que vivimos, era la superficie de una esfera, en otra dimensión que nosotros no vemos. Si la esfera fuese muy grande, el espacio parecería ser casi plano, y la geometría Euclídea sería una estupenda aproximación sobre distancias pequeñas. Pero nos daríamos cuenta de que la geometría Euclídea no funcionaría para grandes distancias. Como ilustración de esto, imaginemos un equipo de pintores, dando capas de pintura sobre la superficie de una enorme bola. A medida que el grosor de las capas de pintura se incrementa, el área de la superficie crece. Si la bola estuviese en un espacio plano tridimensional, se podría seguir añadiendo pintura indefinidamente, y la bola se haría más y más grande. Sin embargo, se el espacio tridimensional fuera realmente la superficie de una esfera en otra dimensión, su volumen sería enorme pero finito. A medida que se añaden más capas de pintura, la bola llegaría eventualmente a llenar la mitad de la superficie del espacio. Después de eso, los pintores Este ejemplo demuestra que no se puede deducir la geometría del mundo partiendo de sus primeros principios, tal y como los antiguos griegos pensaban. En lugar de eso, hay que medir el espacio en el que vivimos, y descubrir su geometría experimentalmente. Sin embargo, aunque en 1854 el alemán George Friedrich Riemann, desarrolló un modo para describir espacios curvos, permaneció como una parte incompleta de las matemáticas durante 60 años. Podía describir espacios curvos que existiesen en el abstracto, pero no había razones por las que creer que el espacio físico en el que vivimos pudiese ser curvo. Esa idea llegó solo en 1915, cuando Einstein presentó la Teoría General de la Relatividad. |
|
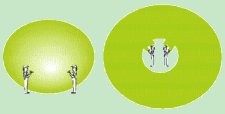descubrirían que están atrapados en un región cuyo tamaño siempre decrece, y casi la totalidad del espacio, estaría ocupado por la bola, y sus capas de pintura. De modo que descubrirían que viven en un espacio curvado, y no plano.