| Tipos de Geometrías y sus diferencias por Jennifer Pérez Aguilera Alumna de 4º de ESO del IES Antonio de Mendoza |
||
|
Una velada en que todos los presentes estén absolutamente de acuerdo…
es una velada perdida -Albert Einstein-. |
||
| En su sentido moderno, la geometría no se ocupa del estudio concreto del espacio físico, aunque desde el punto de vista genético las propiedades que estudia arranquen en último extremo de la intuición geométrica ordinaria. Su cometido estriba mas bien en elaborar espacios abstractos dotados de determinadas características que formalicen rigurosamente aspectos de aquella intuición. Existen, pues, diferentes tipos de geometría que se distinguen entre si bien por la naturaleza de sus postulados, bien por el carácter de las propiedades o relaciones investigadas:
1. Geometría analíticaSe funda en el establecimiento de una correspondencia biunívoca entre los puntos de la recta y los números reales. Elegidos entonces unos ejes de coordenadas, todo punto del espacio está unívocamente determinado por una terna de números; de esta manera los problemas geométricos se convierten en algebraicos. Toda recta, plano, curva o superficie se representa por una ecuación o sistema de ecuaciones cuyo estudio equivale al del elemento geométrico. Actualmente se ha generalizado con el concepto de espacio abstracto n-dimensional (n mayor que 3), que tiene muchas aplicaciones en física; por ejemplo, el espacio de Minkowski cuatridimensional (la cuarta dimensión, el tiempo), empleado en relatividad.
4. Geometría proyectivaEstudia las propiedades de las figuras geométricas que son invariantes a través de una transformación proyectiva. El concepto fundamental es el de espacio proyectivo, ampliación del espacio ordinario añadiendo los elementos impropios: punto impropio es la dirección de una recta; recta impropia es la orientación de un plano; plano impropio es el determinado por un punto y una recta impropia. Las propiedades de incidencia del espacio proyectivo verifican el principio de dualidad. 5. Geometría métricaLas propiedades de que se ocupa este tipo de geometría son las que permanecen invariantes por los desplazamientos, esto es, las distancias y los ángulos. Históricamente, este tipo de geometría ha sido el mas investigado, y con él la regla y el compás han desempeñado un papel privilegiado. Las figuras fundamentales de la geometría métrica plana son el triángulo y la circunferencia; aquel, por ser el polígono más sencillo gracias al cual pueden descomponerse y estudiarse los demás polígonos; esta, porque es fundamental para la comparación gráfica de ángulos. 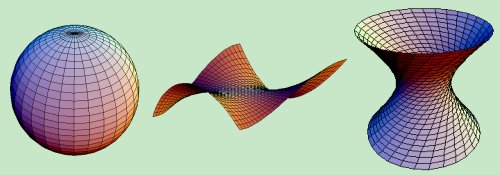 6. Geometría euclídea y no euclídeaEs necesario establecer una distinción entre geometría euclídea, basada en las definiciones, axiomas y postulados de Euclides, y las geometrías no euclídeas, que rechazan el postulado V (“por un punto exterior a una recta pasa una sola paralela a ella”). La geometría no euclídea se divide en:
|
||
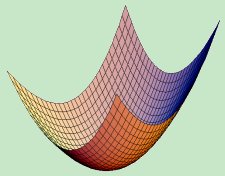 2. Geometría diferencial
2. Geometría diferencial